Coefficients of Form – Ship’s Block, Midship, Waterplane and Prismatic Coefficient
Introduction
Form coefficients of ship refer to coefficients that explain the shape of a vessel through a dimensionless unit. In this article, we shall look at five constants that all naval architects and marine personnel have heard of at some point in their careers.
The five coefficients that we shall cover in this article are as follows:
-
Block Coefficient
-
Midship coefficient
-
Area of waterplane coefficient
-
Prismatic coefficient (aka horizontal prismatic coefficient)
-
Vertical prismatic coefficient
Block coefficient
The block coefficient or Coefficient of Fineness expresses how much a ship resembles a block. A block, in this case, is a cuboidal form with adjacent faces at right angles to each other. The coefficient is denoted by Cb and the formula to calculate it is the ratio of a ship’s volume of displacement to the product of its length, breadth and draft.
Do note that we only consider the vessel portion that is submerged underwater volume.
The coefficient lies between 0 and 1 where 1 resembles the shape of a perfect block. Thus, ships such as tankers and bulk carriers that have fuller hull forms have higher block coefficients.
On the other hand, ships such as yachts and container vessels with finer forms have lower block coefficients.
Generally, fine-form vessels are vessels with a block coefficient of < 0.7, medium-form vessels have a block coefficient of approximately 0.7, and full-form is when the block coefficient is > 0.7.
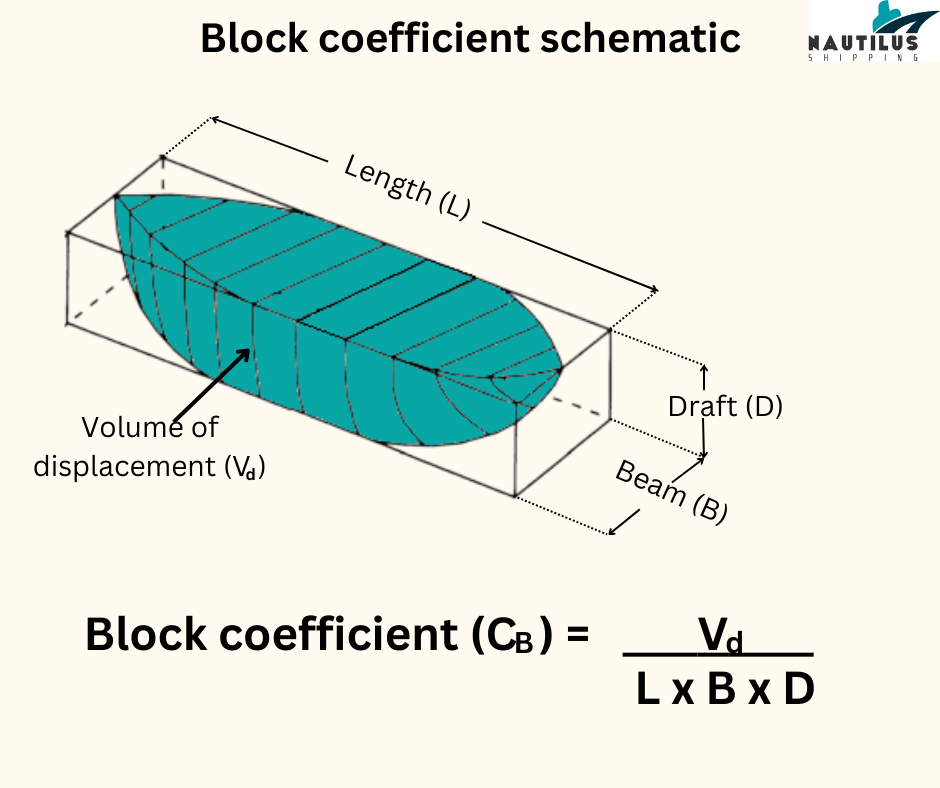
Importance of block coefficient
The block coefficient helps us understand how a hull is shaped. How much of the volume within the block is occupied by the vessel.
The block coefficient is a very important factor in determining various vessel specifications. A fuller hull generates more resistance and therefore, lowers the speed of a ship. This is why container vessels are generally faster than oil tankers.
Besides speed, the block coefficient can also affect the fuel consumption of a vessel. A higher block coefficient requires more fuel to move the ship.
But the block coefficient is also directly related to how much usable volume is available within the ship. This is very important as this is where the ship will store cargo. Reducing the cargo volume will have a greater impact on a ship’s feasibility than the excessive fuel consumption because of a higher block coefficient.
Thus, it is very important to optimise a ship’s block coefficient in the design stage to ensure that we reach a satisfactory trade-off among the above factors.
Midship coefficient
The midship section coefficient can be understood as a 2D version of the block coefficient. It is expressed as the area of the submerged midship section (Am) divided by the product of the draft (D) and beam (B) at the midship section area.
The fuller a ship is at the midship, the higher its midship section coefficient. Like the block coefficient, the value of the midship coefficient lies between 0 and 1.
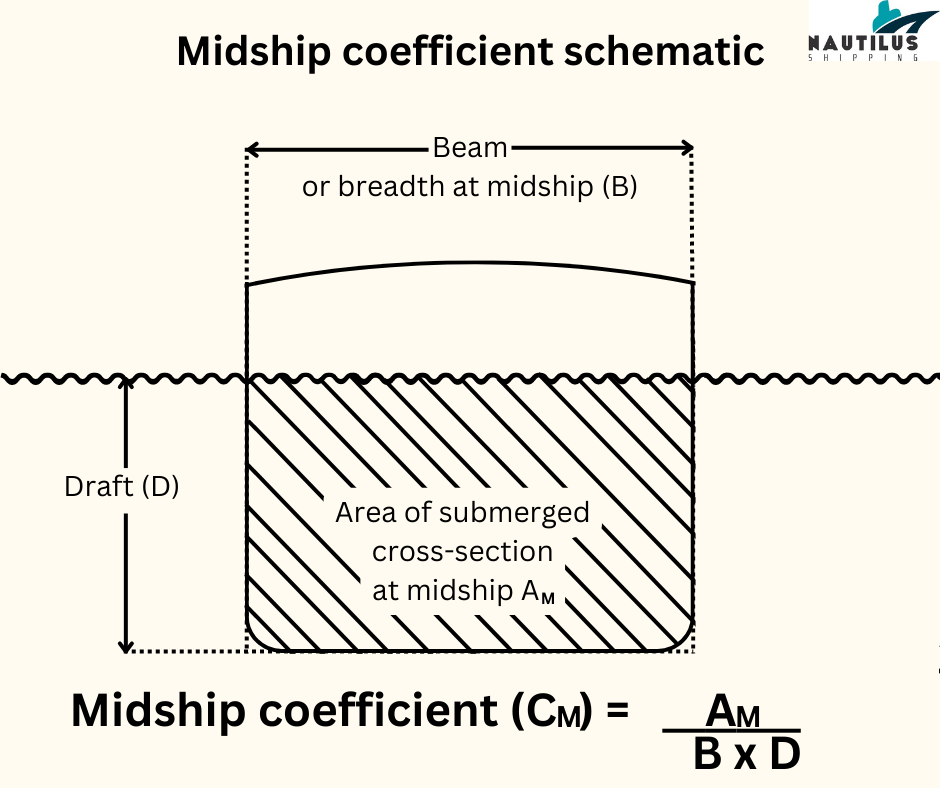
The midship coefficient also has an influence on a variety of important ship-related factors.
If the midship section coefficient increases without an increase in the block coefficient, the frictional and separation resistance increases. This is because the wetted surface area increases as well as the unevenness in velocity distribution becomes greater. But the increase in resistance is relatively small, usually only a few percentage points.
A higher midship coefficient also reduces the need for plate curvature from the keel to the ship’s main deck as well as along the parallel middle body. This reduces the need for frame bending but only for a small area.
Roll damping is another advantage of a high midship coefficient. Ships that have a lower midship coefficient undergo higher rolling compared to those with a higher midship coefficient.
Waterplane area coefficient
The line along the side of the ship where its hull meets the water surface is known as the waterline. If we were to cut the ship along the waterline and remove the top portion, what would be visible is the waterplane.
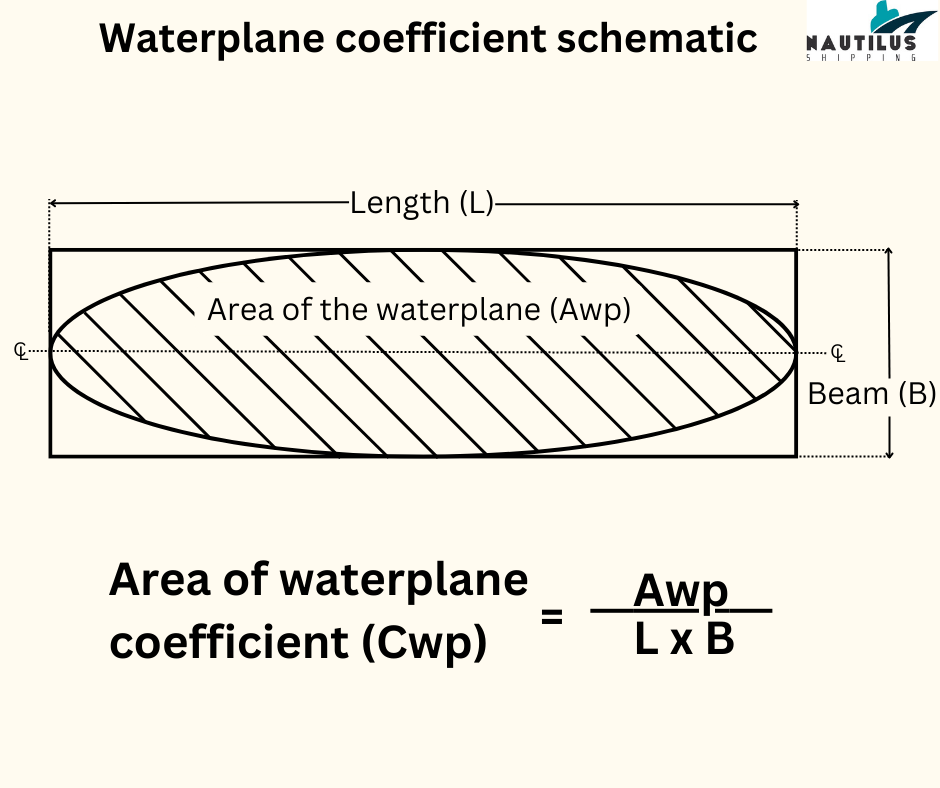
The waterplane area changes with the draft as we move from the keel to the rail. The waterplane area coefficient shows how similar is the ship’s waterplane to a rectangular block of the same length and beam at a particular draft.
The more a waterplane resembles a rectangle, the higher is its waterplane coefficient. A higher waterplane coefficient gives greater stability to a vessel. This may, however, cause increased distortion in the lines.
As a result, when designing a vessel, it is a common practice to choose a lower waterplane area coefficient that matches with other specfications. Then we can design the lines independently. A lower water plane coefficient provides finer ends and lowers the resistance.
Prismatic coefficient
The prismatic coefficient shows how the volume of a vessel is distributed along its length. A lower prismatic coefficient is indicative of finer ends. Similarly, a higher prismatic coefficient shows fuller ends at the forward and aft.
The value of prismatic coefficient also lies between 0 and 1.
Sailboats have a prismatic coefficient of about 0.45 whereas fuller ships such as ULCC tankers can have a prismatic coefficient of more than 0.85. The prismatic coefficient is directly responsible for the wave production by the vessel.
It is calculated by dividing the volume of displacement by the product of the ship’s midship cross sectional area and the ship’s length.
Since the area of a ship’s midship section is smaller than a rectangular block made from the beam and draft at midship, the value of prismatic coefficient is always greater than the block coefficient for a specific vessel.
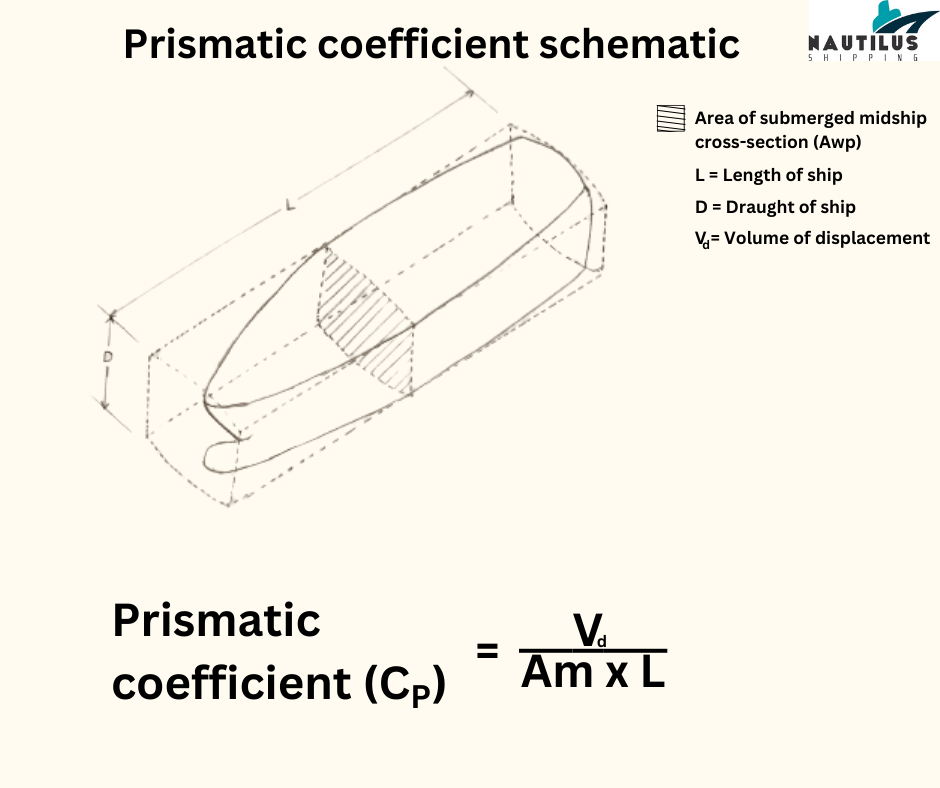
In the above diagram, the shaded portion represents the area of midship section. This section is multiplied by the length of the ship. The volume of displacement is divided by the product of the midship section area and the length to find the prismatic coefficient.
Since we extend the prism along the length of the vessel, the prismatic coefficient is also known as the longitudinal prismatic coefficient.
Vertical prismatic coefficient
The vertical prismatic coefficient is the vertical equivalent of the longitudinal prismatic coefficient.
In vertical prismatic coefficient, instead of a transverse cross-section, we take a vertical cross-section. Just as the longitudinal prismatic coefficient shows the longitudinal distribution of hull along the length, vertical prismatic coefficient shows the vertical distribution of hull from the waterline up to the keel.
Using this coefficient, we can calculate the vertical center of buoyancy to establish the initial stability of the vessel.
To obtain the vertical prismatic coefficient, we divide the volume of displacement by the product of the water plane area and the draft.

Conclusion
These coefficient of form are also known as hull coefficients because they give an overall idea about the shape and distribution of the hull’s underwater volume.
With just the hull coefficients of a ship, it is possible to determine a lot of aspects that will influence a ship significantly over its life.
Some of these include its cargo capacity, resistance, fuel consumption, speed, normal working draft and so on. On the other hand, a lower coefficient provides a lot of disadvantages as well.
Each value has its specific applications and benefits.
For instance, as a ship becomes fuller, the resistance usually increases in the water. But evidence suggests that there are optimum values of these coefficients and that the resistance increases on either side, at least in the case of prismatic and block coefficients.

